|
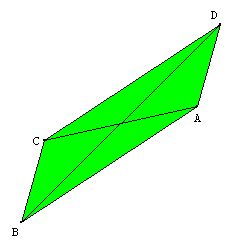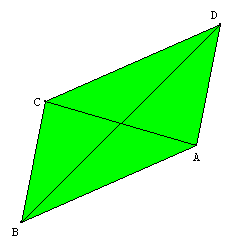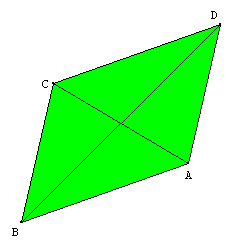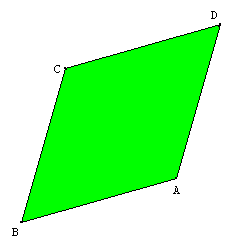
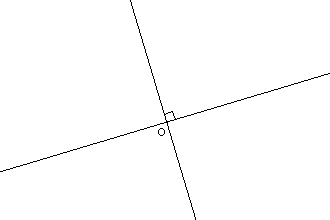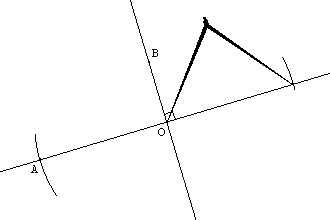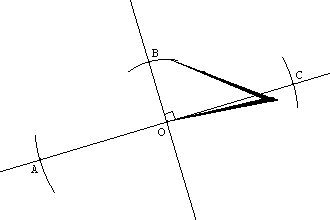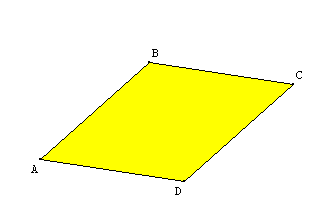
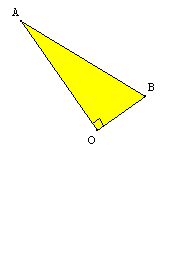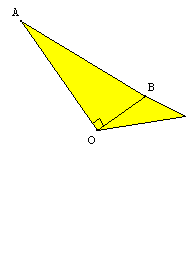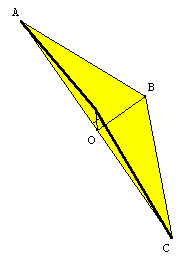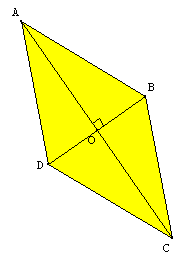
Soient 2 points A et B du plan. On place un point D sur le cercle de centre A et de rayon AB. On a donc AB=AD. On trace les cercles de centre B et D de rayon AB. On appelle C leur point d'intersection autre que A. On a ainsi AB=BC=CD=DA ; le quadrilatère ABCD est un losange. |
"ABCD est un losange" signifie que AB=BC=CD=DA.
Les losanges possèdent donc les propriétés des parallélogrammes.
|
Un losange est un parallélogramme ayant deux côtés consécutifs de même longueur.
Réciproquement, un parallélogramme ayant deux côtés consécutifs de même longueur est un losange. Animation : ABCD est un parallélogramme. Si AB=AD, alors ABCD est un losange. |
|
Un losange est un parallélogramme dont les diagonales sont perpendiculaires.
Réciproquement, un parallélogramme, dont les diagonales sont perpendiculaires, est un losange.
|
Construction : On trace deux droites perpendiculaires en O. Sur chaque droite, on place respectivement un point A et un point B. Puis on construit leur symétrique par rapport à O. ABCD est donc un parallélogramme dont les diagonales sont perpendiculaires, alors ABCD est un losange. |
|
Dans un losange:
|
|
){kind=link}
){kind=link}
){kind=link}
){kind=link}